Overfitting happens when we learn some patterns which do not exist because we have too many sources to learn from. Our entire learning process consists of recognizing patterns and deriving rules from them. Usually these rules help us to plan ahead and make better decisions. But we are so good in finding patterns that we sometimes see them in the wrong places.
Given that something bad happens to you on three different days. It so happens that on each of these days you have seen a black cat at some time. Being an incredible pattern matching engine, your brain tries to create a rule from these observations: black cats mean bad luck. If it had not been the black cat, there would likely be some other circumstance occurring on each of these three days which you could associate with your bad luck. This is a classical instance of overfitting. Each of the thousands of small random events happening every day could be used to explain the bad luck events for which you only have very few instances.
Statistical models and machine learning algorithms can become superstitious in the same way humans do. If our model has too many variables but only a few observations from which the model can be learned, the algorithm may pick up some patterns which are not part of reality.
Example
As an example I will show you how to "predict" the number of deadly traffic accidents in Lithuania from the size of the Amazon rain forest, the population of Germany and the GDP of Australia. It seems obvious that we should not get a meaningful model based on these data. Our dataset looks as follows:
| Year | Accidents | Mio. km² r. forest | Pop. in Mio. | GDP in Bn. USD |
|---|---|---|---|---|
| 2002 | 697 | 3.485 | 82.49 | 394.3 |
| 2003 | 709 | 3.459 | 82.53 | 466.5 |
| 2004 | 752 | 3.432 | 82.52 | 612.9 |
| 2005 | 773 | 3.413 | 82.47 | 693.3 |
| 2006 | 759 | 3.399 | 82.38 | 747.2 |
We will start by using the first three rows (years 2002 - 2004) for training a simple linear model. This turns out to be
If we use this model to predict the 2005 accidents we get 773.6 accidents. Quite accurate so everything is fine, isn't it?
No, nothing is fine. Having n data points and n variables (which are the other three data sets) will allow us to fit almost anything perfectly. To get a correct model from such a setting is incredibly unlikely. To make things worse, in this case all data sets follow a linear trend until 2005. This way even its prediction for 2005 is correct - a very bad coincidence. Using the model for 2006 we get 788.6 accidents which is not so good anymore. And its predictions will get even worse afterwards, as the model has in fact no predictive power at all due to overfitting.
Prevent overfitting
What can be done to prevent overfitting? For machine learning algorithms we can use a technique called regularization. It works by setting up a penalty for the models complexity. If more terms are included in the model the penalty should increase. If we have many observations from which to train the model, this term becomes smaller in comparison to the error term of the model. This way the model can become more complex if we have a lot of data to back it up.
When talking about having more data to prevent overfitting this means having more data regarding to the target we want to predict. In the example it would help to add data for more years. Just adding any other data (more columns with other statistics) will actually make things worse.
Regularization is not the cure-all
While regularization helps in preventing the symptoms of overfitting it does not cure the root cause which is poor understanding of the system that we try to model. The big hazard of big data comes with us trying to create models of something without developing a deeper understanding of the system producing the data. In such cases even the best machine learning models may become superstitious.
Take the financial crisis of 2007. Looking at the housing prices (for example through the lens of the Case-Shiller index) before 2007 one would conclude that housing prices do only increase or stay about the same (there is a very slight down turn in 1990, but its not enough to really qualify as an example for falling prices):
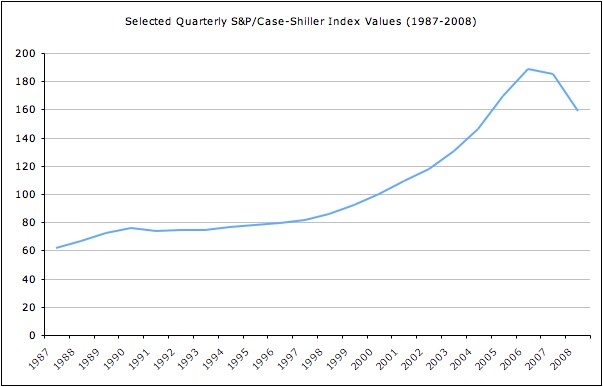
As there simply is no example of falling housing prices in this data set a direct model could not learn how to predict such an event. In fact even human experts have mostly failed to foresee that the ongoing trend might stop. One could say that failure in understanding the underlying system let to overfit models which at some point failed miserably. The people who made a profit from the financial crisis where those who understood the economic systems well enough to conclude that the trend could not be sustained for much longer and prices had to return to a point where they could be sustained by the rest of the economy.
Note that this is not a case where we have too little data. The event we want to predict simply has not happened yet and therefore no amount of data will make sure that a simple model (a linear regression for example) will be able to make accurate predictions for these unseen events.
Test for overfitting
A way to see if your model might be overfitted is to use a test set. In the example we excluded the years 2005 and 2006 from training the model. This way we could use them to validate the model. In the example we saw that the test set should be sufficiently large, the year 2005 would have been insufficient to detect the models bad behavior.
Its important that the test set is used once and only once. Assume you train a model, try it on the test set and see that it is bad. You then tweak some parameters, retrain and test again. Repeating this process you arrive at an acceptable model. Guess what - you just introduced overfitting again. This time you adjusted your hand tuned parameter to the test set. And the worst part: You do not have another test set to see that you screwed up. Therefore it is important to handle the test set with great care.
Conclusion
When working with large amounts of data (of which we have a lot more at our disposal by now) it is important to remain wary of conclusions drawn from the data. This is especially true when these conclusions are created using automated systems like machine learning algorithms. Models that are not based upon deeper understandings of the underlying system have the potential to pick up the wrong signals and to perform badly in the future. Mistaking correlation for causation, generalizing short term trends or having too many variables and too little data (the classical overfitting) are just some of the mistakes that lead us to wrong models. To prevent these problems we have to put in more work to properly understand what really happens in a model and if its predictions are based on sound reasoning.
Header photo by Faris Algosaibi
comments powered by Disqus